Bien podríamos decir que medir es asignar una cantidad (cuantificar) a una magnitud física en una escala a través de un instrumento de medición. Pero eso solo sería pensar de manera muy limitada.
En ciencia, medir no solo significa “dar un número”, sino comparar una magnitud con otra del mismo tipo que tomamos como referencia: una unidad. Según el Vocabulario Internacional de Metrología (VIM, 2012), medir es "obtener experimentalmente uno o varios valores que pueden atribuirse razonablemente a una magnitud" (VIM, 2012, sec. 2.1, p. 61). Dicho de forma simple: medir es comparar algo con una unidad conocida y expresar cuántas veces contiene esa unidad.
Por ejemplo, si decimos que una varilla mide 20 cm, decimos que su longitud es equivalente a la veinte veces lo que mide un “centímetro”.
La metrología es la ciencia de las mediciones y sus aplicaciones. Se encarga de establecer los principios, métodos y normas que permiten obtener mediciones confiables y comparables, asegurando que los resultados sean congruentes, no importa dónde, cuándo o quién lo haga.
Los sistemas de unidades son un conjunto de medidas estándar que sirven para medir magnitudes de longitud, masa, tiempo, fuerza y más. Establece las unidades que son fundamentales, cómo se relacionan entre sí. Gracias a los sistemas de unidades, distintas personas y laboratorios, incluso pueden comparar resultados de mediciones sin ambigüedad.
Una unidad es un patrón de medición de una maginitud física, cuyo propósito es cuantificar cierta magnitud física que presenta un objeto medido en relación a su tamaño de la misma magnitud.
En la afirmación "la mesa tiene una longitud de 2 metros." Longitud es la magnitud que estamos cuantificando y metro la unidad con la que estamos comparando. Literalmente "esta cosa mide tantas de esas cosas". Por supuesto, esto abre las posibilidades a la imaginación para decir cosas como: "La Facultad de Ciencias mide $x$ campos de fútbol", o "... mide $y$ canchas de tenis"; pero estas unidades un tanto arbitrarias no nos son muy útiles, por tanto, hay que estandarizar más generalmente.
El Sistema Métrico Decimal (SMD), creado a finales del siglo XVIII en Francia, introdujo la idea de emplear unidades estándar reproducibles y, sobre todo, la característica de utilizar múltiplos, los prefijos basados en potencias de 10: deca (101), hecto (102) y kilo (103); y los submútiplos: deci (10−1), centi (10−2), mili (10−3). Lo que simplificó las conversiones dando coherencia al sistema.
Dato curioso: el metro fue definido por primera vez en 1791 como la diezmillonésima parte de la longitud de la línea que conecta el Polo Norte con el ecuador pasando por el Observatorio de París. En la actualidad se define como la distancia que recorre la luz en 1 ∕ 299792458 segundos, siendo ésta la misma distancia, pero ahora definida con base en una constante física universal.
El Sistema Internacional de Unidades (SI) es la evolución moderna, ampliada y rigurosamente estandarizada del Sistema Métrico Decimal. Conserva su esencia decimal, incluidos los prefijos métricos heredados del SMD y muchos otros añadidos posteriormente, como micro (10−6), nano (10−9), mega (106) o giga (109), pero la expande mediante un marco mucho más completo que integra siete unidades base, unidades derivadas coherentes y definiciones fundamentadas en constantes físicas universales. El SI convierte la estructura métrica en un sistema científicamente reproducible y universal.
Los prefijos del SMD y del SI están organizados en pasos de 10, lo que coincide con nuestro sistema de numeración indoarábigo. Gracias a ello, una medición expresada en distintas submúltiplos, por ejemplo: 1 metro, 5 decímetros, 3 centímetros y 2 milímetros se escribe como 1.532 m. Esta coincidencia es una de las grandes fortalezas del SMD y de su evolución moderna, el SI.
Son las unidades fundamentales a partir de las cuales se construyen todas las demás:
Desde el año 2019, cada unidad del SI se define fijando el valor exacto de una constante fundamental. El metro se define a partir de la velocidad de la luz ($c$), el segundo a partir de la frecuencia de transición del átomo de cesio y el kilogramo a partir de la constante de Planck. Esto asegura que sean invariables, reproduibles y exactas en cualquier lugar del universo, reforzando la estructura decimal heredada del Sistema Métrico Decimal.
Velocida de la luz: \[c = 299,792,458~\frac{\text{m}}{\text{s}}\]
Segundo: \[1s = \text{tiempo que tardan 9,192,631,770 oscilaciones del átomo de} ~ ^{133}\text{Ce}.\]
Kilogragmo: \[1\text{kg} = \left( \frac{h}{6.62607015 \times 10^{-34}} \right)\qquad ;\] donde $h = 6.62607015~~\text{kg}\cdot\text{m}^2\cdot\text{s}^{-1}$
Las unidades derivadas se obtienen a partir de combinaciones algebraicas de las unidades base. Aunque muchas de estas unidades no existían formalmente en el Sistema Métrico Decimal original, su coherencia y su estructura algebraica siguen la misma lógica decimal introducida por aquel sistema.
Las unidades derivadas se obtienen a partir de combinaciones de las unidades fundamentales. Por ejemplo, el newton (N) es la combinación de kilogramo, metro y segundo, expresado como: \[N = \text{kg}\cdot\text{ms}\cdot\text{s}^{-2}\qquad;\] el joule (J) es Newton por metro: \[J = \text{N}\cdot\text{m}\] y el pascal (Pa) es: \[\text{Pa} = \frac{\text{N}}{\text{m}^2}\]
El SI mantiene y amplía los prefijos introducidos por el SMD para representar múltiplos y submúltiplos de las unidades de manera sistemática. A estos se suman muchos otros desarrollados posteriormente para suplir otras necesidades: como micro, nano, mega, giga, tera, pico y más recientemente ronna o quetta. Estos prefijos expresan valores de medición o muy pequeños o muy grandes.
A diferencia del SI y del SMD, el Sistema Imperial Inglés no está organizado mediante múltiplos de 10. En su lugar, utiliza relaciones históricas entre unidades. Por ejemplo:
En la actualidad, los únicos países que aún usan en su mayoría el Sistema Imperial Inglés son: Estados Unidos, Liberia y Birmania; excepto en contextos de enseñanza científica, donde se alinean al SI. Mientras que países como Reino Unido y Canadá usan en algunas situaciones de la vida el Sistema Imperial Inglés y en otras el SI.
Estas relaciones no decimales complican las conversiones, ya que requieren memorizar valores específicos en lugar de aplicar reglas uniformes de potencias de diez. Por esta razón, una cantidad expresada en pies, pulgadas y fracciones (como 5′ 7½″) no se puede escribir en una sola expresión decimal compacta sin realizar las conversiones necesarias.
Para el Sistema Imperial Inglés, las unidades, que son por ejemplo: pulgada, cuarto de pulgada y octavo de pulgada; hay que convertir estas fracciones a decimales y sumarlas; mientras que en el SI, sus submúltiplos permiten sumar directamente sin hacer conversiones molestas, con en nuestro ejemplo de 1.532 m.
Consejo: El detalle de "... en relación a su tamaño de la misma magnitud" en la definición antes mencionada de unidad es muy importante y es lo que nos lleva al concepto de coherencia de unidades. No podemos medir la longitud de la Facultad de Ciencias en grados centígrados o en amperios. Eso no tiene ningún sentido, pues estas son unidades de otras magnitudes físicas, y no de longitud. Si no hay coherencia en la unidades, eso puede fácilmente descartar la validez de una ecuación física:
"Las unidades de lo que tengas del lado izquierdo deben ser la unidades de lo que tengas del lado derecho."
Según el VIM, una escala de un instrumento visualizador (o dispositivo que “muestra” una magnitud) es la parte que consiste en un conjunto ordenado de graduaciones (y normalmente valores numéricos) usadas para indicar la magnitud medida (VIM, 2012, sec. 4.1, p. 67).
Dicho de otra forma, cuando ves un instrumento con líneas graduadas ( o "marcas") y números (como un termómetro, un voltímetro analógico o una regla), esa colección ordenada de graduaciones y valores es lo que se le llama escala.
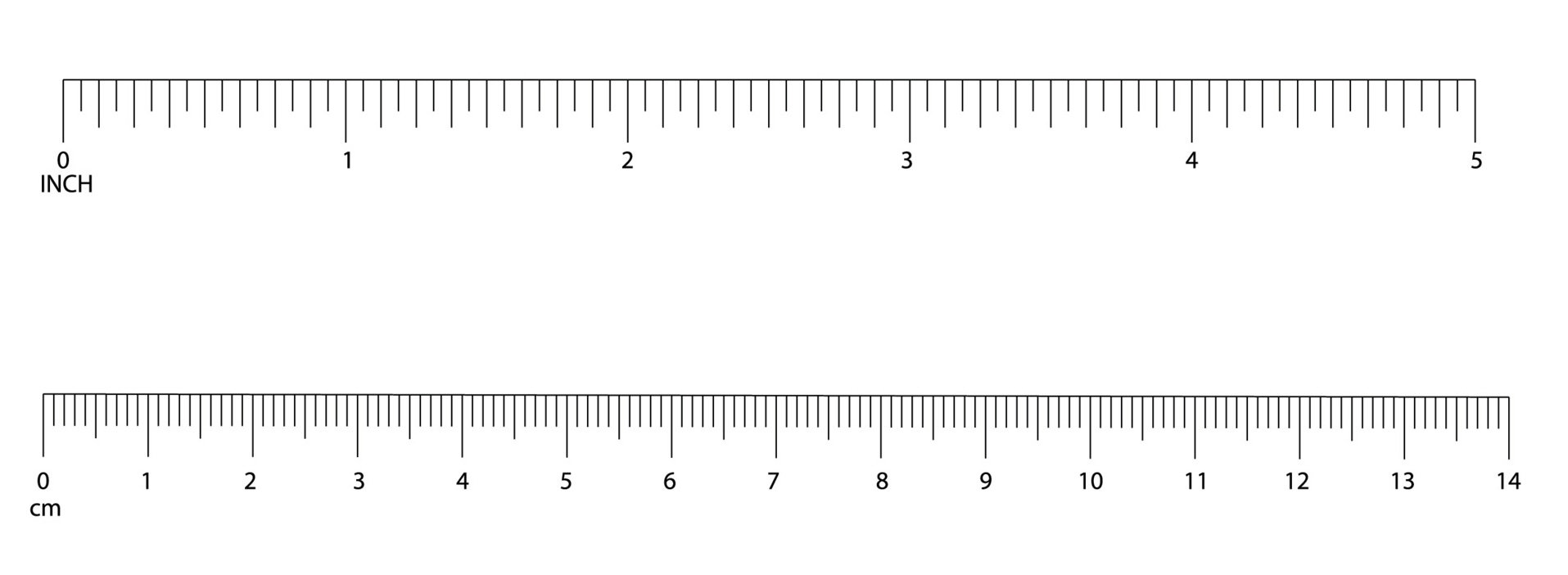


Seguro que ya sabes medir con una regla común y corriente. Simplemente presentas el objeto o uno de los lados del objeto por medir extendido paralelo a la regla. En la escala de una regla las graduaciones grandes representan centímetros (cm) y las pequeñas milímteros (mm). Ahora bien, ¿qué pasa si el extremo del objeto medido queda justo en medio de dos graduaciones de mm? ¡Esta pregunta es muy imporante y da la base de la idea de lo que después llamaremos incetidumbre! Por ahora, digamos que siempre tomarás la más pequeña de las dos graduaciones.
Nota: en la siguiente guía "marca" hace referencia a una línea identificadora de color colocada sobre una graduación en la imagen, sin embargo, en este contexto pueden usarse graduación y marca de manera intercambiable. En el habla coloquial del laboratorio "división" de una escala, o incluso "rayita" suelen usarse entre universitarios.
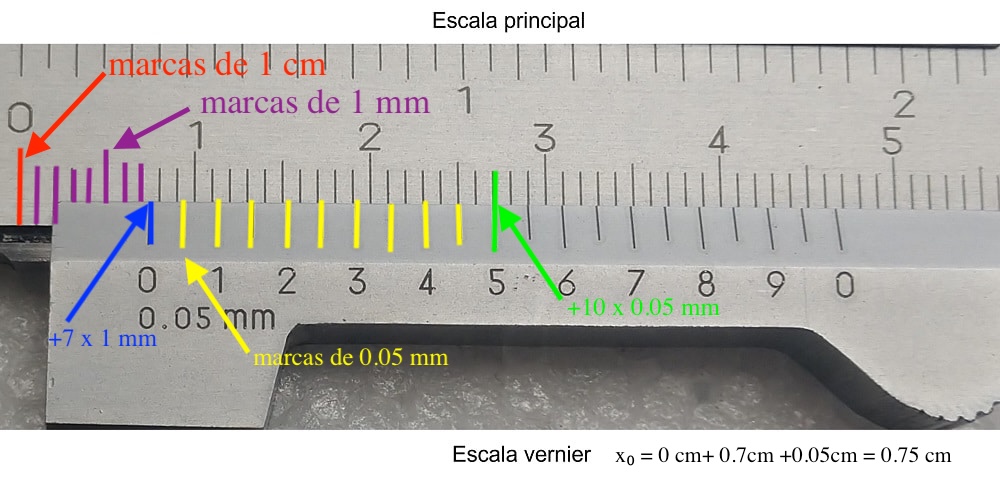
Observa la Figura 4. Pasos para medir con un calibrador con Vernier:
Observa la Figura 5. Pasos para leer la escala de un micrómetro:

Ahora bien, te aseguro que por lo menos una vez al medir una longitud con una regla o flexómetro la medida que querías tomar quedo entre dos graduaciones más pequeñas de la escala, entonces, como ya dijimos antes: ¿tomamos la menos como valor medido... y ya? ¿Es todo? Pues resulta que no, que eso no es todo: hay cierta duda sobre cuál es la medida real. Aunque la longitud del objeto quede "exactamente" sobre una de las graduaciones de nuestra escala, eso solamente de acuerdo a nuestros ojos, la realidad es que siempre hay una incerteza o incertidumbre sobre cuál es el valor real de la medición.

Una incertidumbre de una medición es un valor que nos da un rango que asegura una muy alta probabilidad de la existencia de la medida real dentro de sí. (De acuerdo con la Probabilidad más rigurosa y pura, nunca se garantiza por completo por más grande que sea el rango, pero eso es un poco demasiado teórico para nuestros propósitos.) El tamaño de la incertidumbre depende del instrumento con el que se realizó la medición, y a veces también del tamaño de la medición misma.
En metrología se distinguen dos ideas importantes:
Como explica Stephanie Bell (A Beginner’s Guide to Uncertainty of Measurement, 2001), "una medición no está completa si no se acompaña de su incertidumbre" . Por eso, en el laboratorio siempre que se mida algo debe estimarse también este margen de duda.
En la GUM (Guide to the Expression of Uncertainty in Measurement, JCGM 100:2008), la notación
\[ x = x_0 + \delta x \qquad (1.1) \]
se utiliza para describir el modelo matemático de una medición, donde cada magnitud de entrada se representa como un valor de referencia más una pequeña desviación. La sección 4.1.3 define el modelo general:
\[ Y = f(X_1, X_2, \dots, X_N) \qquad (1.2) \]
y establece que cada magnitud de entrada puede expresarse como:
\[ X_i = x_{0,i} + \delta X_i \qquad (1.3) \]
La sección 5.1.2 de la GUM explica que esta forma permite calcular cómo las pequeñas variaciones \(\delta X_i\) se propagan y afectan al resultado final \(Y\). Cada término tiene un significado específico dentro del marco de la GUM:
Sabiendo que tanto $x_0$ como $\delta x$ tienen unidades de las magnitudes físicas que se midieron, es natural la notación donde se "factorizan" las unidades:
\[x = (x_0 \pm \delta x)\textbf{u} \qquad (1.4);\]donde $\textbf{u}$ son las unidades de la magnitud en cuestión.
Supongamos que medimos la longitud de una barra y obtenemos la medición 10.0 cm El promedio de esas mediciones se toma como el valor mejor estimado:
\[ x_0 = 10.0~\text{cm} \]
Si representamos la longitud verdadera como en (1.1), entonces \(\delta x\) es una pequeña diferencia (en un momento veremos un criterio para determinar cuánto es $\delta x$ exactamente) que indica cuánto podría apartarse el valor real de la media. El modelo de la GUM considera precisamente estas pequeñas desviaciones \(\delta x\) para determinar la incertidumbre combinada.
Podemos imaginar
El valor medido \(x_0\) se encuentra en el centro del intervalo, mientras que el valor verdadero \(x\) se espera dentro del rango \([x_0 - \delta x,\, x_0 + \delta x]\).
Toda medición tiene cierto margen de duda, incluso cuando se usa un instrumento de alta calidad y resolución muy fina. Esta duda se debe a diversas causas, principalmente del instrumento de medición usado, por ejemplo: la resolución misma, calibración, desgaste, etc.
En la siguiente lección veremos algunos factores que introducen error, y cómo afecta directamente a las incertidumbres considerar eso. Hay condiciones del ambiente: temperatura, humedad o iluminación, viento, etc. Está también el propio observador: principalmente diferencias en la apreciación o en la lectura de la escala, algunos factores fisiológicos del observador que dificulten su lectura del instrumento, etc. Por ahora, concentrémonos en medir con nuestros intrumentos.
Imagina que estás midiendo la longitud de una mesa cuya longitud real es: \[ L = 150.0~\text{cm} \] Utilizas una regla que, sin que lo notes, tiene un defecto de fabricación: todos los centímetros están comprimidos ligeramente: la regla marca menos longitud de la real. Tú haces varias mediciones independientes y obtienes: 149.2 cm, 149.3 cm, 149.2 cm y 149.3 cm. Estas medciones son precisas, porque se parecen mucho entre ellas, pero no exactas, porque NO se parecen al valor real.
En palabras simples: si hay poca diferencia entre las medciones, hay precisión.
Si hay poca diferencia entre las mediciones y el valor de referencia., hay exactitud.
Puede ocurrir que haya una, la otra, las dos o ninguna.
En los laboratorios de física, cada magnitud que obtengas debe expresarse con su incertidumbre. Esto permite saber qué tan confiable es el resultado y comparar tus datos con los de otros equipos o con valores teóricos.
IMPORTANTE: seguramente escucharás a tus compañeros y profesores usar la palabra precisión
en otro sentido
para comparar las mínimas escalas o resluciones de los intrumentos, por ejemplo:
Una balanza granataria tiene una "precisión" (mínima escala) de $0.1\text{g}$, mientras que una analítica
tiene una "precision" de $0.001\text{g}$. Por lo que se dice que la balanza analítica es más "precisa"
que la granataria.
Este uso, que aunque no concuerda con la definición estadística de la palabra precisión que acabamos de dar y que habla sobre cuando hay poca dispersión de los datos, es muy común de escuchar en el habla coloquial tanto fuera como dentro del laboratorio.
Un valor de referencia es aquel que sirve como base para comparar o verificar resultados de medición. Puede ser el valor asignado a un patrón, un material de referencia o un valor aceptado por consenso como representativo de una magnitud. En la práctica, es el “valor verdadero” al que se intenta aproximar la medición.
A veces también se le denomina valor nominal. Por ejemplo: una resistencia marcada como “100 Ω” tiene ese como valor nominal, pero su valor real podría ser 99.8 Ω o 100.3 Ω según su tolerancia.
Este nombre, sin embargo, trae ambigüedad respecto a la definición que presentamos anteriormente. Así que, informalmente los términos valor de referencia y valor nominal a veces se usan de manera intercambiable para significar un valor que se tiene como una base comparativa, por lo que en esta guía no usaremos el término valor nominal y usaremos el término valor de referencia. También en esta guía a $x_0$ le llamaremos valor medido. Finalmente, le llamaremos valor experimental ($x_{\text{exp}}$) al valor de una magnitud que se obtiene como resultado final de un experimento.
¿Cómo sabemos qué incertidumbre tomar? Este criterio es aplicable por defecto si no se cuenta con un manual de uso del instrumento donde el fabricante haya recomendado una incertidumbre específica por asociar (a veces anexo a un certificado de calibración). El criterio de la mínima escala, sin embargo, para nuestros propósitos y para alinearse con los estándares internacionales está incompleto. IMPORTANTE: Más adelante veremos el concepto de distribución rectangular y cómo complementa este criterio.
Si medimos algo con una regla, notamos que la escala está dividida en cm y mm, y ya no hay divisiones más pequeñas, decimos entonces que la mínima división de su escala, o simplemente su mínima escala, es de 1 mm.
Nuestro instrumento nos garantiza que la medición no excede dos graduaciones sucesivas de milímetros, así pues, la incertidumbre es igual a la mitad de la mínima escala: en este caso, medio milímetro (0.005 cm). Volvamos al ejemplo de la Figura 3:
Cuando un instrumento no tiene subdivisiones más pequeñas entre 40.3 cm y 40.4 cm, no podemos saber en qué parte de este espacio se encuentra el valor real.
Ese límite no tiene que ver con que el ojo no vea más, sino con que el instrumento no proporciona información suficiente para justificar una mayor precisión .
Por eso la regla usual es:
\[ \delta x = \frac{\text{mínima escala}}{2} = \frac{a}{2} \qquad (1.5)\](La notación $a$ para representar la mínima escala se usará en la siguiente lección.)
En nuestro caso
Aunque visualmente parezca estar un poco a la derecha, no hay manera de comprobar si está en 40.31, 40.33, 40.36 o 40.38 cm. Todas esas mediciones dan prácticamente la misma impresión visual, porque el instrumento no tiene graduaciones más pequeñas que 0.1 cm. Los instrumentos analógicos se deja a la interpretación del ojo humano debido a que solo entregan información limitada por sus graduaciones.
Lo único seguro es que la medición está entre 40.3 y 40.4 cm, pero no sabes qué tan cerca de cada extremo.
Como no tenemos forma de asignar una posición más precisa, no hay otra opción más que suponer que el valor real está entre esas dos divisiones (distribuido uniformemente, esto se verá en la Lección 5).
Si visualmente decides que la medición es 40.3 cm porque parece más cerca de esa graduaciónque de 40.4 cm, entonces:
Por tanto, el intervalo garantizado es: [40.25 cm, 40.35 cm]
Por eso, metrológicamente no es recomendable reportar 40.36 cm porque sería una exactitud falsa, pero sí puedes reportar 40.3 ± 0.05 cm, que cubre la realidad física sin exagerar la precisión.
El criterio de ± mitad de la mínima escala no describe exactamente lo que ves, sino lo que realmente puedes asegurar con la resolución del instrumento.
El criterio de la mitad de la mínima escala garantiza que:
Finalmente, la medición de la Figura 3 se reporta como:
\[ x = (40.3 \pm 0.05) \text{cm} \]
No porque la línea esté exactamente ahí, sino porque es el mejor conocimiento posible con un instrumento de resolución de 1 mm.
Sin embargo, si deliberadamente escoges reportar una cifra mayor a 40.3 cm porque insistes que es evidente entre las graduaciones y decidiste realizar un estimado, puedes hacerlo. Esta idea se llama cifra apreciada, y debe ser siempre reportada subrayada. Por ejemplo: si insisto en confiar en mi ojo y reportar "40.36 cm" como valor medido, debo hacerlo como \( (40.3\underline{6} \text{cm} \pm 0.05) \text{cm}\). Te romendamos no abusar de las cifras apreciadas.
Veamos otro ejemplo:Al medir un cuaderno de forma francesa con una regla de 50 cm, obtenmos 14.8 cm de ancho y 21.0 cm de largo. Estas medidas deben de reportarse con incertidumbre así: $(14.8 \pm 0.05)\text{cm}$ y $(21.0 \pm 0.05)\text{cm}$.

En general, la notación (1.4) puede variar dependiendo de la magnitud física medida, pues a lo que se refiere $x$ en esta notación es la magnitud real de un magnitud física cualquiera al realizar su medición, y sus componentes, de su respectivo valor medido e incertidumbre asociada, y puede ser sustituida por el símbolo de dicha magnitud. Por ejemplo:
Supongamos que el ancho real del cuaderno del ejemplo anterior es $14.826 \ \text{cm}$, sin embargo, debido a la resolución limitada de nuestro instrumento obtenemos una medida de $14.8 \ \text{cm}$. Llamamos a 1, 4 y 8 las cifras significativas. Una cifra significativa es cualquier dígito que contribuye a la precisión de una medición. Aquí están los 5 criterios para identificar cifras significativas:
Ahora un ejemplo no tan sencillo. ¿Qué tal 0.0045600 ? Para identificar las cifras significativas tenemos que:
1. Quitar ceros a la izquierda: los tres primeros ceros (0.0045600) solamente marcan posición, no cuentan.
2. Dígitos distintos de cero: el “4”, el “5” y el “6” sí cuentan.
3. Ceros intermedios: ninguno aquí.
4. Ceros finales con punto decimal: los dos últimos ceros (“00”) están después de un dígito distinto de cero y con punto decimal, por tanto sí cuentan.
Entonces 0.0045600 tiene 5 cifras significativas: (4, 5, 6, 0, 0). Observa que la cifra apreciada aquí sería el último cero:
está estimada dentro de la resolución del instrumento que generó esa lectura.
Otro ejemplo: $7.890 \times 10^4$
En notación científica, siempre se escribe la cantidad de cifras significativas de forma explícita.
Aquí los dígitos son: 7, 8, 9, 0 → 4 cifras significativas.
El $\times 10^4$ solamente indica la escala (mueve el punto decimal), no afecta al conteo de cifras significativas.
Entonces $7.890 \times 10^4$ tiene 4 cifras significativas.
La cifra apreciada es el cero final, que fue añadido porque el instrumento permitió estimar con esa precisión.
Veamos un último ejemplo: la cantidad de $13.59 \ \text{cm}$, medida con un calibrador con Vernier cuya mínima escala es $0.01 \ \text{cm}$ tiene 4 cifras significativas: 1, 3, 5 y 9; puesto que en éste pueden leerse hasta las centésimas de centímetro, e implícitamente se está considerando que la medida real existe en un intervlo que va desde $13.585 \text{cm}$ hasta $13.5195 \ \text{cm}$.
Ya conocemos el criterio de la mínima escala. Recuerda que si no contamos con un manual de uso del instrumento donde se especifique qué incertidumbre se debe asociar a cada medición, por defecto usaremos este criterio. Y en el laboratorio, una medición no está completa sin su incertidumbre. Ahora un poco de práctica:

$V = ($ $\pm$ $)~\text{v}$

$T = ($ $\pm$ $)~^{\circ}C$

$T = ($ $\pm$ $)~^{\circ}C$
¿Qué pasa si al medir una longitud realizamos 3 mediciones con tres de diferente preción cada uno, y queremos saber la longitud total? Pues tendremos que sumar, es decir:
Este resultado debe reportarse con las cifras significativa de la medición menos precisa. Para reducir entonces las cifras de nuestra longitud total, recurrimos al redondeo, empezando por las cifras de más a la derecha.
a) Si la última cifra es menor a 5, la eliminamos (se trunca). Ejemplo: redondeemos 12.42 a 3 cifras significativas.
$\require{cancel}$ $12.42 \rightarrow 12.4\cancel{2} \rightarrow 12.4$b) Si la última cifra es mayor a 5, se elimina y a la penúltima se le suma 1. Ejemplo: redondeemos 18.36 a 3 cifras significativas.
$18.36 \rightarrow 18.\cancelto{4}{3}\cancel{6} \rightarrow 18.4$c) Si la última cifra es 5, tenemos dos casos:
Caso 1: si la penúltima cifra es un número par, el 5 se elimina. Ejemplo: para 22.45.
$22.45 \rightarrow 22.4\cancel{5} \rightarrow 22.4$Caso 2: la penúltima cifra es un número impar, el 5 se elimina y a la penúltima cifra se le suma uno. Ejemplo: para 22.75.
$22.75 \rightarrow 22.\cancelto{8}{7}\cancel{5} \rightarrow 22.8$Así entonces, retomando nuestro ejemplo de la longitud total obtenida por una suma, tenemos:
(Se recomienda aplicar el redondeo ya a la suma, es decir, al total, y no a los sumandos.)
Como la medición menos precisa es a 3 cifras significativas, redondearemos la longitud total a 3 cifras significativas.
En $70.635$ la última cifra es 5, por lo que aplicamos el criterio especial para el 5: como la penúltima cifra es impar se le suma 1 y el 5 se elimina.
$~~\rightarrow 70.6\cancelto{4}{3}\cancel{5} \rightarrow ~~ 70.64$.De aquí aplicaremos el redondeo una vez más para llegar a las 3 cifras significativas. Como la última cifra es 4, que es menor a 5, se trunca y obtenemos:
$70.6\cancel{4}\rightarrow~$ $70.6$Hasta ahora se han mencionado varias deficiones y conceptos que se utilizarán en las siguientes lecciones. Puedes consultar aquí un Glosario de definiciones para las deficiones de los conceptos importantes mencionados en todas las lecciones.
Las citas en el texto con la forma “(VIM, 2012, sec. X.Y, p. Z)” corresponden a definiciones oficiales del Vocabulario Internacional de Metrología (JCGM 200:2012). Se incluyen con fines educativos para señalar la fuente de cada concepto técnico utilizado en esta lección.