Ahora que ya sabemos procesar los datos de nuestro experimento obtenidos en el laboratorio para obtener sus respectivas incertidumbres, debemos aprender a elaborar gráficos para representarlos visualmente de manera correcta. Esto para confirmar que el comportamiento de las variables es el esperado. Trabajaremos únicamente con gráficos 2D, es decir, gráficos que representen el comportamiento de una variable con respecto a otra ( (x,y) o «variable 1 vs variable 2»).
A veces los valores asociados a una variable son muy grandes respecto a los valores de la otra, incluso órdenes de magnitud más grandes. Para poder representar nuestros datos de tal forma que quepan dentro de nuestro gráfico, introduciremos el gráfico logarítmico.
El gráfico logarítmico en un eje o semilogarítmico es aquel que sobre uno de sus ejes las unidades incrementan de manera lineal unitaria, unidad por unidad, mientras que sobre el otro las unidades incrementan de manera exponencial en potencias de 10, es decir, por ejemplo, mientras que sobre el eje $x$ las unidades incrementan hacia la derecha de manera normal: 1, 2, 3, 4...; sobre el eje $y$ incrementan: 1 ($10^0$), 10 ($10^1$), 100 ($10^2$), 1,000 ($100^3$)...; y se llama logarítmico y no exponencial porque el eje se ve como si hubiéramos tomado el logaritmo de cada uno de esos números ($\log_{10} 1 = 0$, $\log_{10} 10 = 1$, $\log_{10} 100 = 2$, $\log_{10} 1,000 = 3$, ...), lo que causa que el crecimiento exponencial del eje $y$ se vea como un crecimiento lineal unitario.
Las barras de error o barras de incertidumbre son las líneas que se dibujan sobre los puntos de una gráfica para mostrar qué tanto puede variar una medición. Indican el rango donde probablemente se encuentra el valor real del dato. Al graficar resultados experimentales, deben dibujarse sus barras de incertidumbre (en ambas direcciones), excepto que su trazo resulte imperceptible. Su tamaño depende del error estimado en cada eje (por ejemplo, en tiempo o distancia) y ayudan a ver si los datos son consistentes con sus errores. Además, sirven para comprobar que la dispersión media de los puntos alrededor de la mejor recta sea de magnitud semejante a la incertidumbre media de los puntos.
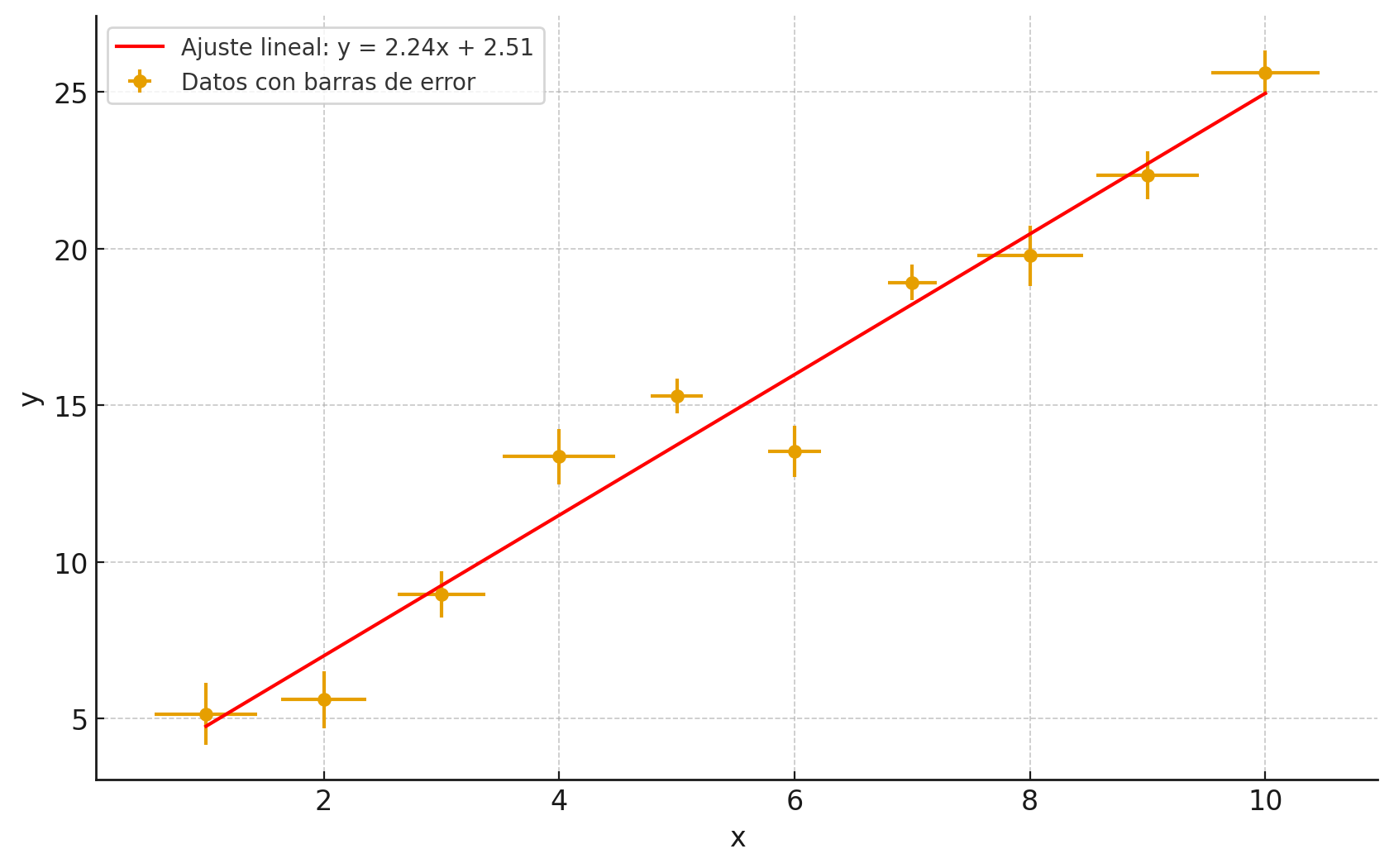
Las barras se extienden tanto sobre el eje vertical como sobre el horizontal lo grande que sea el rango de incertidumbre en cada eje. Estas barras, que forman rectángulos de incertidumbre, representan una zona de confianza: aunque no se sepa exactamente cuál es el punto “verdadero” o “más probable”, “se puede afirmar, con razonable seguridad, que está contenido en el rectángulo”. Por eso, la línea o curva que mejor se ajuste a los datos no tiene que pasar justo por el centro de cada punto, sino dentro de los márgenes que marcan las barras. Esto es importante porque permite ver de manera rápida la calidad de las mediciones, comparar resultados con los valores teóricos y juzgar si el ajuste que se obtuvo tiene sentido o no. [2]
En una gráfica experimental en general, la zona de incertidumbre es el área que muestra el margen dentro del cual se espera que se encuentren los valores verdaderos del fenómeno medido, considerando las incertidumbres asociadas a los datos o al modelo.
Esta zona se construye a partir de los límites superior e inferior del ajuste —por ejemplo, las curvas o rectas obtenidas al sumar y restar la incertidumbre al valor ajustado—, y visualmente se representa como una franja sombreada alrededor de la curva teórica.
Su función es doble: Indicar la precisión del modelo, es decir, qué tan estrecha o amplia es la confianza en los resultados del ajuste. Y permitir una interpretación visual inmediata: los puntos experimentales deberían caer, en su mayoría, dentro de esa franja si las incertidumbres fueron correctamente evaluadas.
Aquí verás dos ejemplos de gráficas con zonas de incertidumbre.
En nuestros experimentos ejemplo los conjuntos de puntos que representan los datos d elas variables medidas forman dos tipos de curvas: una lineal para el primer experimento, y una tres hiperbólicas para el segundo. Esto se nota en las ecuciones que describen el fenómeno observado:
\[ V = RI ~~~~ (6.1) \]
Este es el despeje que queremos para nuestra gráfica, ya que el voltaje (V) será el eje $y$, mientras que la intensidad de corriente (I) será el eje $x$. Queda entonces la resistencia (R) como un simple escalar multiplicando a I, es decir, una pendiente que aproximaremos con un simple método numérico que se explica en el libro Datos y reporte en el Laboratorio de Mecánica (2002) de René Garduño [1]. Este método es útil para aproximar funciones lineales (rectas) del tipo $y = mx + b. ~~~~ (6.2)$
Paso 1: Ubiquemos nuestro conjunto de puntos $P = \{p_i\} = \{(x_i,y_i)\}$ con $i = 1, 2, 3, ..., n$, donde $n$ es la cardinalidad de nuestro conjunto, la cuál debe ser un número par. Así que te recomendamos tomar un número par de mediciones que sea, por buena práctica, por lo menos 10. En este caso tenemos $n = 20$. Se da también por supuesto que, ya que lo que se quiere es proponer una función $y = y(x)$, ordenes tus mediciones de manera creciente o decreciente respecto a las coordenadas $y$, ya que suponemos una recta. En este caso la recta es creciente.
Paso 2: Partimos nuestro conjunto en dos subconjuntos $P = P_1 \cup P_2$, donde $P_1$ es la primera parte de nuestro conjunto, es decir, para nuestro caso, los primeros 10 puntos (Recordemos que $n$ es la cardinalidad de nuestro cunjunto original $P$. $n/2$ = 10), y $P_2$ nuestra segunda mitad, es decir, del punto 11 al 20: $P_1 = \{p_i\} = \{(x_i,y_i)\}$ con $i = 1,2,3,...,10$ y $P_2 = \{p_j\} = \{(x_j,y_j)\}$ con $j = i+10 = 11,12,13,...,20$.
Paso 3: Calcularemos ahora $n/2$ pendientes diferentes. Recuerda que una pendiente ($m$) no es más que «cuánto avanzo sobre el eje $y$ sobre cuánto avanzo sobre el eje $x$» con los avances desde un punto a otro. Para esto usaremos los puntos a pares de la siguiente forma: al primer punto de $P1$ le toca asociarse con el primero de $P_2$, es decir, calcularemos la pendiente $m_1$ entre el $p_1$ y el $p_{11}$, después la pendiente $m_2$ entre $p_2$ y $p_{12}$, después $m_3$ entre $p_3$ y $p_{13}$ y así sucesivamente hasta tener las 10 $m$. Entonces las pendientes $m$ son de la forma:
\[m_i = \frac{y_j - y_i}{x_j - x_i}\] con $i = 1,2,3,...,10$ y $j = i + 10$
Paso 4: Ahora que tenemos las 10 pendientes, vamos a calcular una pendiente promedio $\bar{m}.$
\[ \bar{m} = \sum_{i=1}^{n/2} m_i ~~~~ (6.3)\]
Y también calcularemos la incertidumbre de le pendiente. Así es, la pendiente misma también lleva una incertidumbre asociada dada por la siguiente ecuación:
\[ \delta m \approx \frac{5}{4} \sum_{i=1}^n |m_i - \bar{m}| = 0.0004\]. Finalmente:
\[I(V) = (0.0103 \pm 0.0004)V - 0.0013 \]
Paso 5: la ecuación que tenemos que utilizar es: $\bar{y} = \bar{m}\bar{x} + b. ~~~(6.4)$ Donde $\bar{y}$ y $\bar{x}$ son la coordenadas $y$ y $x$ promedio de todos nuestros puntos del conjunto original $P$. Entonces, las calculamos como cualquier otro promedio:
\[ \bar{x} = \frac{1}{n}\sum_{i=1}^{n} x_i ~~~~ (6.5)\] y \[ \bar{y} = \frac{1}{n}\sum_{i=1}^{n} y_i ~~~~ (6.6)\]
Una vez teniendo estos valores, solo hace falta calcular la $b$, que es dónde cortará la recta al eje $y$.
Paso 6: despejamos la $b$ de la ecuación $(6.4)$, que en este caso es $b = -0.0013$. Así pues obetenemos la aproximación lineal:
\[ y = 0.0103 x - 0.0013 \]
Puedes consultar todos los cálculos en la hoja de cálculo descargable:Con la gráfica en el formato de la Ley de Ohm \(I\) vs. \(V\) (es decir, \(y=I\), \(x=V\)), la recta ajustada tiene pendiente promedio \(\bar{m} = \Delta I/\Delta V\). Dado el valor \(\bar{m} = 0.01026\ \text{A/V}\), la resistencia se obtiene como el inverso de la pendiente porque \(I=\frac{1}{R}V\Rightarrow m=\frac{1}{R}\). Por tanto, \(R = \frac{1}{\bar{m}} = \frac{1}{0.01026}\ \Omega \approx 97.47\ \Omega\). Esta aproximación puramente numérica no es tan buena como promediar los datos experimentales.
A continuación se presenta código en Python para graficar nuestro Experimento Ejemplo 1.
Si nunca has programado antes, no te preocupes: Python es un excelente punto de partida. Es un lenguaje de programación moderno, gratuito y muy usado en la ciencia, la ingeniería y el análisis de datos. Con Python puedes automatizar cálculos, graficar tus mediciones y analizar tus resultados experimentales sin depender de hojas de cálculo o software complicado.
Para empezar a usar Python no necesitas instalar nada. Google ofrece una herramienta gratuita llamada Google Colab, que funciona directamente en tu navegador y te permite programar de manera interactiva.
Piensa en Colab como un cuaderno de laboratorio digital, donde puedes escribir texto, fórmulas y código en la misma página. Cada bloque se llama celda. En una celda escribes código, y para ejecutarlo basta con presionar Shift + Enter. El resultado aparecerá justo debajo: puede ser texto, números o una gráfica.
Esto te permite avanzar celda por celda, verificando tus resultados paso a paso, igual que en el laboratorio físico: mides, anotas, analizas, y luego interpretas. Puedes agregar comentarios, guardar tu notebook en Google Drive y retomarlo más tarde desde cualquier computadora.
Puedes ir copiando los bloques uno a uno y compilarlos en tu notebook.
import numpy as np
import math
import matplotlib.pyplot as plt
# =============================================
# PASO 1: INGRESAR LOS DATOS EXPERIMENTALES Y SUS INCERTIDUMBRES
# Puedes reemplazar estos valores por los de tu propio experimento.
# =============================================
P = [
(2.0,0.020),
(2.5,0.026),
(3.0,0.029),
(3.5,0.036),
(4.0,0.041),
(4.5,0.044),
(5.0,0.052),
(5.5,0.054),
(6.0,0.066),
(6.5,0.066),
(7.0,0.073),
(7.5,0.076),
(8.0,0.083),
(8.5,0.088),
(9.0,0.091),
(9.5,0.097),
(10.0,0.104),
(10.5,0.101),
(11.0,0.115),
(11.5,0.119)
]
x = np.array([p[0] for p in P], dtype=float)
y = np.array([p[1] for p in P], dtype=float)
# Incertidumbres de cada variable
dx = 0.05/math.sqrt(3)
dy = 0.0005/math.sqrt(3)
#En caso de que hagas una gráfica donde la incertidumbre varíe punto a punto puedes reemplazar las dos líneas de dx y dy por:
# dx = np.array([])
# dy = np.array([])
# Y dentro escribir las incertidumbres de cada punto por cada eje separadas por comas, y usar justo después:
# dx = np.divide(dx, math.sqrt(3))
# dy = np.divide(dy, math.sqrt(3))
#Para dividir los todos los elementos del vector entre raíz de tres, SI FUERA NECESARIO.
# ==============================================================================
# PASO 2: VERIFICAR QUE HAY UN NÚMERO PAR DE PUNTOS Y DIVIDIR LOS PUNTOS EN DOS MITADES
# =============================================================================
n = len(x)
if n % 2 != 0:
raise ValueError("El número de puntos debe ser PAR para usar este método.")
# =============================================
# PASO 3: FORMAR LOS PARES Y CALCULAR LAS PENDIENTES INDIVIDUALES
# =============================================
pendientes = []
for j in range(n//2):
dy_j = y2[j] - y1[j]
dx_j = x2[j] - x1[j]
m_j = dy_j / dx_j
pendientes.append(m_j)
pendientes = np.array(pendientes)
# =============================================
# PASO 4: CALCULAR LA PENDIENTE PROMEDIO Y SU INCERTIDUMBRE
# =============================================
m = np.mean(pendientes)
incertidumbre_m = (5/4) * np.mean(np.abs(pendientes - m))
# =============================================
# PASO 5: CALCULAR EL PUNTO PROMEDIO Y LA ORDENADA AL ORIGEN
# =============================================
x_prom = np.mean(x)
y_prom = np.mean(y)
b = y_prom - m * x_prom
# =============================================
# PASO 6: ECUACIÓN DE LA RECTA
# =============================================
if (b > 0) or (b == 0):
ecuacion = f"y = {m:.5f}x + {b:.5f} ±{incertidumbre_m:.5f}"
else:
ecuacion = f"y = {m:.5f}x {b:.5f} ±{incertidumbre_m:.5f}"
# =============================================
# PASO 8: GRAFICAR CON BARRAS DE ERROR VARIABLE
# =============================================
x_linea = np.linspace(min(x) - 0.5, max(x) + 0.5, 200)
y_linea = m * x_linea + b
plt.figure(figsize=(10, 6))
plt.errorbar(x, y, xerr=dx, yerr=dy, fmt='o', color='blue',
ecolor='gray', elinewidth=1, capsize=3, label='Datos experimentales')
plt.plot(x_linea, y_linea, color='red', label=ecuacion)
plt.title('V vs I aplicados en una resistencia')
plt.xlabel('Voltaje (V)')
plt.ylabel('Intensidad (I)')
plt.grid(True)
plt.legend()
plt.tight_layout()
plt.show()
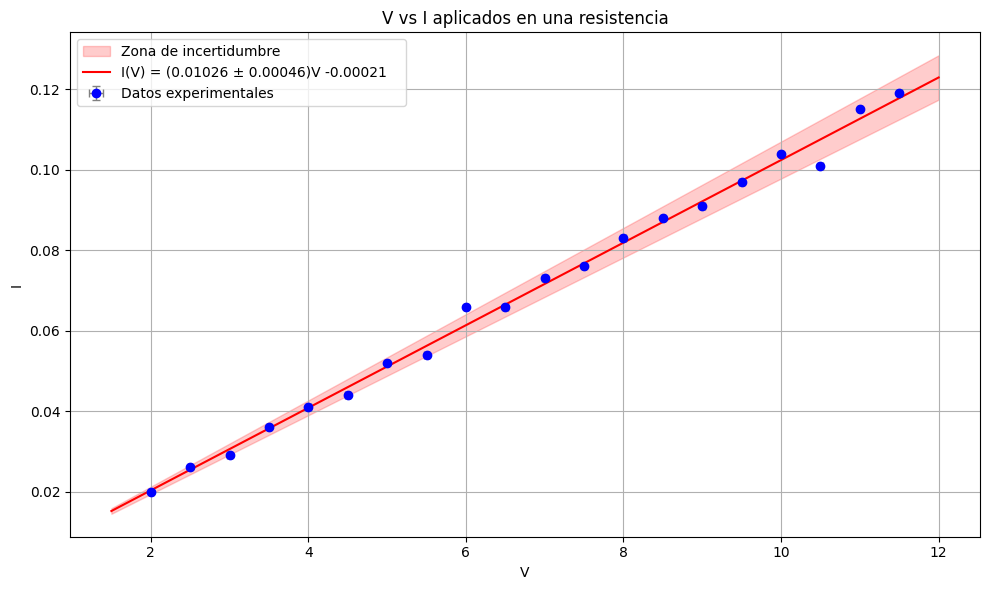
Con la gráfica y aproximación de nuestros puntos, podemos dar por concluido el análisis de datos del Experimento 1
Grafiquemos los resultados de nuestro Experimento Ejemplo 2. Los puntos obtenidos en el gráfico con ejes ($f$ vs $\lambda$) son:
${(40.3,850) , (36.2,950), (32.8, 1050), (30.4,1150), (27.6,1250), \\ (25.6,1350), (23.8,1450), (22.3,1550), (20.9,1650), (20.9,1750)}$
Este método aproxima funciones del tipo $y(x) = \frac{a}{x}$ donde a es una constante. Queremos calcular esta $a$. En nuestro Experimento Ejemplo 2 donde calculamos experimetalmente la velocidad del sonido en distintos gases. Tenemos que:
\[ v = \lambda f ~~ \rightarrow ~~ f(\lambda) = \frac{v}{\lambda} ~~~~(6.7);\]
que es una función hiperbólica como $\frac{1}{x}$ multiplicada por una constante $v$ que es la velocidad del sonido, es decir $y = f$, $x = \lambda$ y $a = v$. Aproximemos pues esta función:
Paso 1: ubiquemos nuestro conjunto de puntos $P = \{p_i\} = {(x_i,y_i)}$ con $i = 1,2,3,..., n$ donde n es de nuevo cuántos puntos tenemos. En este caso $n$ no está restringido a ser un número par, pero aún así hemos tomado 10. $n = 10$.
Paso 2: sea el conjunto $LP_x$ el conjunto de los logaritmos naturales de las coordenadas $x$ de cada uno de los puntos de $P$.
\[ LX = \{ lx_i \} =\{ln(x_i)\} ~~ \text{con} ~~ i = 1,2,3,...,n\]
Lo mismo para las coordenadas $y$.
\[ LY = \{ly_j\}= \{ln(y_j)\} ~~ \text{con} ~~ j = 1,2,3,...,n \]
Paso 3: ahora calculemos la suma de estos logaritmos naturales. Sea
\[ S = \{s_i\} = \{ lx_i + ly_j \} = \{ ln(x_i) + ln(y_i) \} ~~ \text{que también se puede ver como} ~ = \{ ln(x_i y_i) \} \]
Paso 4: promediemos estas sumas.
\[ ln(a) = \bar{s} = \sum^n_{i=1} s_i ~~~~ (6.8)\]
Paso 5: calculemos $a$ con la exponencial de este número.
\[ a = e^{\bar{s}} \approx 34,718.26 = v\]
Debido a las unidades que se usaron para las mediciones esta $v$ está dada en $\text{cm/s}$, así que nuestra aproximación de $v$ sería $347.1826 ~~ \text{m/s} = 1,249.85736 ~~ \text{km/h}$
¿Y qué pasa con la incertidumbre dle parámetro $a$ aquí? Pues, adaptando el razonamiento de Garduño:
\[ \delta a \;=\; \frac{5}{4}\, a \,\overline{\bigl|\,\ln a_i - \overline{\ln a_i}\,\bigr|} ~~~~ (6.10)\] donde: \[ \ln a_i = \ln x_i + \ln y_i, ~~~~(6.11) \qquad \overline{\ln a_i} = \frac{1}{n}\sum_{i=1}^{n} \ln a_i.~~~~ (6.12) \]La barra superior sobre estas expresiones representa, como ya se ha visto en otras ocaciones, un promedio de todos los valores que puede tomar sobre el contador $i$. Tomar $+\delta a$ y $- \delta a$ nos delimitará nuestra zona de incertidumbre en nuestra gráfica.
Paso 6: solo falta proponer la función y graficarla.
mport numpy as np
import matplotlib.pyplot as plt
import math
# -------------------------------------------------------
# 1) Datos experimentales
# -------------------------------------------------------
P = [
(850, 40.3),
(950, 36.2),
(1050, 32.8),
(1150, 30.4),
(1250, 27.6),
(1350, 25.6),
(1450, 23.8),
(1550, 22.3),
(1650, 20.9),
(1750, 20.9),
]
x = np.array([p[0] for p in P], dtype=float)
y = np.array([p[1] for p in P], dtype=float)
# -------------------------------------------------------
# 2) Incertidumbres constantes para barras de error
# -------------------------------------------------------
dx = np.array([0.1085,0.1095,0.1105, 0.1115, 0.1125, 0.1135, 0.1145, 0.1155, 0.1165, 0.1175])
dy = 0.05
# Y dentro escribir las incertidumbres de cada punto por cada eje separadas por comas, y usar justo después:
# dx = np.divide(dx, math.sqrt(3))
# dy = np.divide(dy, math.sqrt(3))
# -------------------------------------------------------
# 3) Linealización logarítmica: ln(y) = ln(a) - ln(x)
# -------------------------------------------------------
lnx = np.log(x)
lny = np.log(y)
ln_a_i = lnx + lny # cada valor individual de ln(a)
ln_a_hat = ln_a_i.mean() # promedio de ln(a)
a_hat = np.exp(ln_a_hat) # parámetro estimado
# -------------------------------------------------------
# 4) Incertidumbre del parámetro a según Garduño (Ecs. 1.3 y 1.4)
# -------------------------------------------------------
# Residuales
residuos = ln_a_i - ln_a_hat
# Desviación estándar aproximada (Ecuación 1.3)
s_ln_a = (5/4) * np.mean(np.abs(residuos))
# Incertidumbre de a (Ecuación 1.4 adaptada)
da = a_hat * s_ln_a
a_min = a_hat * np.exp(-s_ln_a)
a_max = a_hat * np.exp(+s_ln_a)
# -------------------------------------------------------
# 5) Curva ajustada y zona de incertidumbre ("zona de seguridad")
# -------------------------------------------------------
x_grid = np.linspace(0.95 * x.min(), 1.05 * x.max(), 400)
y_fit = a_hat / x_grid
y_fit_min = a_min / x_grid
y_fit_max = a_max / x_grid
-------------------------------------------------------
# 6) Gráfica con barras de error y zona de incertidumbre
# -------------------------------------------------------
plt.figure(figsize=(8,5))
plt.errorbar(x, y, xerr=dx, yerr=dy, fmt='o', color='blue',
ecolor='gray', elinewidth=1, capsize=3, label='Datos experimentales')
# Zona de incertidumbre en rojo claro
plt.fill_between(x_grid, y_fit_min, y_fit_max, color='red', alpha=0.2,
label="Zona de incertidumbre")
# Curva ajustada
plt.plot(x_grid, y_fit, 'r-', label=f"Ajuste: y = a/x, a ≈ {a_hat:.2f}")
plt.xlabel("f [Hz]")
plt.ylabel("L [cm]")
plt.title("f vs L de onda en aire a 21.6 C y 0.77 atm")
plt.legend()
plt.grid(True, linestyle="--", alpha=0.5)
plt.show()
A continuación, este último bloque es opcional y solo para obetener información adicional del ajuste:
print(f"a estimado = {a_hat:.6f}")
print(f"s_ln(a) (5/4·prom|d|)= {s_ln_a:.6f}")
print(f"δa = {da:.6f}")
print(f"Intervalo (exp) = [{a_min:.6f}, {a_max:.6f}]")
print(f"Relativa δa/a = {s_ln_a*100:.3f}%")
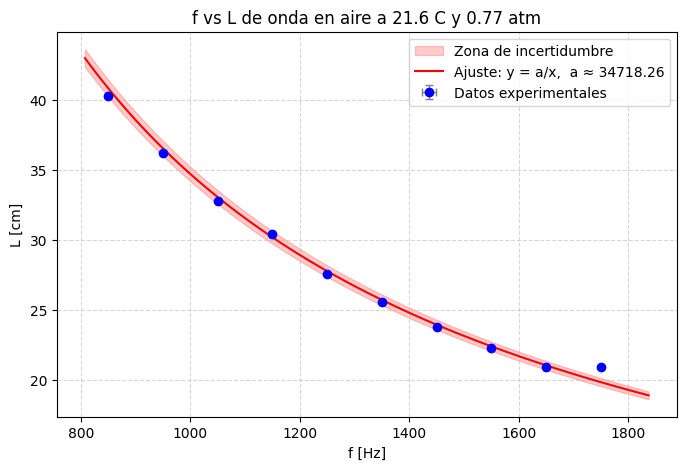
Por supuesto, el universo está lleno de fenómenos que no se pueden modelar con simples funciones lineales o hiperbólicas. En tu camino como estudiante de Física las funciones que te encuentres seguramente sean de los tipos:
Cuadrado inverso: \[ y(x) = \frac{a}{x^2}\]
como la Ley de Coulomb, la Ley de la Gravitación Universal, la intesidad de un sonido, etc.
Polinomios de grado n: \[P_n(x) = a_0 + a_1x + a_2x^2 +...+a_nx^n\]
como Caída Libre, la Ley de Stefan-Boltzmann, la Energía Potencial de Osciladores no armónicos, etc. Y una infinidad de funciones, aunque según su modelo no sean polinomios, se pueden aproximar con polinomios de grado suficientemente alto en una región de la gráfica o igualar a "polinomios de grado infinito" (Series de Taylor). Proponer un polinomio para resolver una ecuación diferencial, dependeindo de los coeficientes, también se le conoce como Método de Serie de Potencias.
Exponencial:
\[y(x) = e^{ax}\]
o bien \[y(x) = b_0 + b_1e^{ax} + b_2 e^{2ax}+...\]
Siempre he dicho cómica y exageradamente que en este universo todo se puede aproximar con una expenencial. Solo es cuestión de encontrar tu parametro $a$ apropiado. Ejemplos hay muchísimos como la carga de un condensador, la desintegración de los núcleos atómicos (radiación), la ley de enfiamiento de Newton, etc.
Si consideramos sumas de exponenciales negativas multiplicadas por senos y cosenos obtenemos todo el movimiento amortiguado (movimiento oscilatorio que disminuyepoco a poco). Y si consideramos las exponenciales complejas, es decir, elevadas a números complejos $a + bi$, ¡podemos modelar todo tipo de cosas que escapan a nuestra imaginación!
Distribución normal: \[f(x) = e^{-ax^2}\]
¡El parámetro $a$ puede complicarse muchísimo para ajustar la ditribución! Este tipo especial de exponencial nos permite modelar fenómenos como fluctuaciones térmicas en sistemas en equilibrio, distribución de velocidades en un gas ideal, etc...
Aproximaciones por series de Fourier: \[ \begin{equation} \begin{split} f(x) = a_0 + a_1 \cos\left( \frac{2\pi}{L} x\right) + a_2 \cos\left(\frac{4\pi}{L} x\right) + ... + a_n \cos\left(\frac{2n\pi}{L}x\right) + \\ + b_0 + b_1 \sin\left({\frac{2\pi}{L}x}\right) + b_2 \sin\left({\frac{4\pi}{L}x}\right) + ... + a_n \sin\left(\frac{2n\pi}{L}x\right)+... \end{split} \end{equation} \]
donde $a_n$ y $b_n$ son de la forma $\frac{2}{L}\int _0 ^{L} f(x)\sin\left(\frac{2n\pi}{L}x\right) dx$ y $\frac{2}{L}\int _0 ^{L} f(x)\cos\left(\frac{2n\pi}{L}x\right) dx$ respectivamente, y $L$ es el periodo de la función.
Estas sirven para modelar señales eléctricas complicadas en circuitos o aparatos electrónicos, o incluso para la distribución de calor sobre una superficie.
Para apredar más sobre cómo aproximar y modelar funciones, te recomendamos los libros:
¡Perfecto! Ya conoces los suficientes fundamentos de la metrología para realizar tu primer experimento y tratar tus datos para calcular sus incertidumbres de acuerdo a los estándares internacionales. Ahora solo faltan unas recomendaciones generales sobre el Laboratorio. Haz click en Para terminar...