El siguiente procedimiento explicativo del tratamiento de los datos va de acuerdo a lo tratado por Stephanie Bell en A Beginner’s Guide to Uncertainty of Measurement [1], quien se apega a la GUM de la JCGM [2].
Supongamos que queremos verificar el valor de la resistencia eléctrica (R) de una resistencia que, según el fabricante, es de 100 $\Omega$ (ohmios). Diseñaremos entonces un experimento sencillo que nos permitirá saber si el fabricante dice la verdad. Necesitaremos los siguientes materiales:
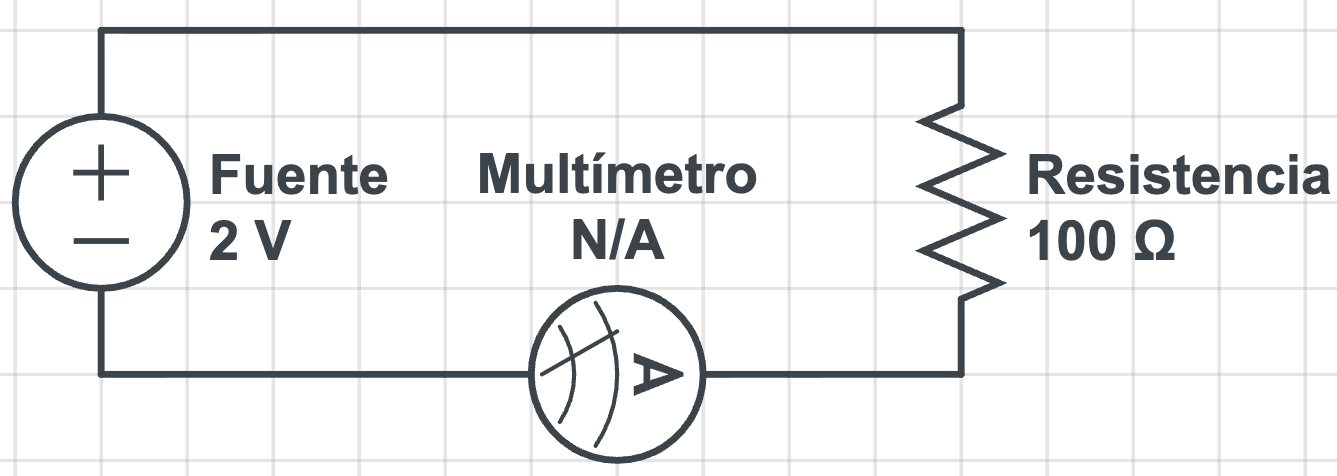
Calculador aritmética de incertidumbres(+) fuente → resistencia → multímetro → (–) fuente.La Ley de Ohm es probablmente la ley más fundamental de la electrónica, y relaciona la diferencia de potencial eléctrico, o voltaje, (V) que es aplicada a los extremos de una resistencia (R) conductora con la intensidad de corriente eléctrica (I) que ésta provoca sobre la misma. La ecuación es:
\[ I = \frac{V}{R} ~~~;\]
donde $I$ es la intensidad de corriente que se mide en amperios (A),
$V$ es el voltaje que se mide en voltios (V)
y $R$ es la resistencia que se mide en ohmios ($\Omega$).
Si despejamos resistencia de la ecuación obtendremos:
\[ R = \frac{V}{I} \]
El $\pm 10 \%$ que aparece en el valor nominal de la resistencia significa que el fabricante promete un valor real de la resistencia que se encuentra entre los 90 $\Omega$ y 110 $\Omega$. A este valor porcentual se le llama tolerancia de la resistencia.
Nuestra tabla tendrá 4 columnas: una comlumna de enumeración (#), que simplemente es para saber cuál es el número de medición; valor de voltaje (V) medido en voltios; valor de intensidad de corriente (I) medido en aperios;
¿Y qué es la última columna $u_c(\text{R})$? Pues es nuestra incertidumbre combinada de la resistencia que aprendimos a calcular en la lección anterior. Recordemos que:
\[u_c (f) = \sqrt{\sum_{i=1}^n \left( \frac{\partial f}{\partial x_i} \cdot u_i \right)^2} ~~; \]y para este caso en específico entonces:
\[u_c (\text{R}) = \sqrt{\left(\frac{u_V}{I} \right)^2 + \left(\frac{V}{I^2} u_I \right)^2} \].Se recomienda primero buscar el manual
No olvides que par este caso las incertidumbres de los instrumentos se dan como la mitad de la mínima escala divida entre $\sqrt{3}$. Entonces:
\[u_V = \frac{0.005}{\sqrt{3}} = 0.00288675... ~~~ \text{y} ~~~ u_I = \frac{0.0005}{\sqrt{3}} = 0.000288675...\]Puedes usar la calculadora de Incertidumbre Combinada para comprobar los resultados numéricos tú mismo. Sólo recuerda seguir las instrucciones de uso ahí anotadas:
Ahora se nos presenta la parte más tediosa del análisis de datos de un experimento: los cálculos de la incertidumbre combinada. Para esto, recomendamos que te apoyes de un programa de hojas de cálculo para el procesamiento de datos numéricos como Microsoft Excel (de paga para Windows, pero disponible gratis con un correo de @comunidad.unam.mx para los alumnos de la UNAM en Software Unam a través de Office 365), Google Spreadsheets (gratis, en línea), Libre Office (gratis, no privativo, para Windows, MacOS y distribuciones de Linux), Numbers (incluido en cualquier dispositivo de Apple), etc.
Te dejamos aquí el archivo .xlsx (hoja de cálculo), que cualquiera de los softwares anteriores mecionados puede abrir, donde se encuentra el procesamiento de datos del experimento y la aplicación de la fórmula de la incertidumbre estándar combinada. Allí verás el procesamiento de los datos, ¡y podrás sustituirlos con tus propios datos de tus propios experimentos a futuro! Haz click en el botón para descargarla:
| # | V ($\pm 0.05\text{V}$) | I ($\pm 0.0005$ A) | R = V/I [$\Omega$] | $u_c(\text{R})$ [$\Omega$] |
|---|---|---|---|---|
| 1 | 2.0 | 0.020 | 100.0 | 2.04 |
| 2 | 2.5 | 0.026 | 96.15 | 1.54 |
| 3 | 3.0 | 0.029 | 103.45 | 1.43 |
| 4 | 3.5 | 0.036 | 97.22 | 1.12 |
| 5 | 4.0 | 0.041 | 97.56 | 0.98 |
| 6 | 4.5 | 0.044 | 102.27 | 0.94 |
| 7 | 5.0 | 0.051 | 98.04 | 0.79 |
| 8 | 5.5 | 0.054 | 101.85 | 0.76 |
| 9 | 6.0 | 0.060 | 100.0 | 0.68 |
| 10 | 6.5 | 0.066 | 98.48 | 0.61 |
| 11 | 7.0 | 0.072 | 97.22 | 0.56 |
| 12 | 7.5 | 0.076 | 98.68 | 0.53 |
| 13 | 8.0 | 0.081 | 98.77 | 0.50 |
| 14 | 8.5 | 0.088 | 96.59 | 0.46 |
| 15 | 9.0 | 0.091 | 98.90 | 0.45 |
| 16 | 9.5 | 0.097 | 97.94 | 0.42 |
| 17 | 10.0 | 0.103 | 97.09 | 0.39 |
| 18 | 10.5 | 0.101 | 103.96 | 0.41 |
| 19 | 11.0 | 0.112 | 98.21 | 0.36 |
| 20 | 11.5 | 0.119 | 96.64 | 0.34 |
Aplicamos los criterios de redondeo necesarios para dejar los resultados expresados con las cifras significativas de la medición menos precisa, como se explicó en la Lección 1. El siguiente paso es promediar los valores de $R$ obtenidos:
\[ \bar{R} = \frac{1}{n} \sum_{i=1}^n R_i = 98.95~\Omega \]
Calculamos la desviación estándar muestral de los valores de resistencia:
\[ \sigma = \sqrt{\frac{1}{n-1} \sum_{i=1}^n (R_i - \bar{R})^2 } = 2.292~\Omega \]
La incertidumbre estándar Tipo A es entonces:
\[ u_A = \frac{\sigma}{\sqrt{n}} = \frac{2.292}{\sqrt{20}} = 0.513~\Omega \]
Cada valor de $R_i$ tiene su propia incertidumbre combinada $u_{c,i}$ (ya calculada en la tabla):
\[ u_{c}(R_i) = \sqrt{\left(\frac{u_V}{I_i}\right)^2 + \left(\frac{V_i}{I_i^2} u_I\right)^2}. \]
Para obtener la incertidumbre asociada al promedio de los resultados, combinamos en cuadratura las incertidumbres individuales de cada iteración:
\[ \text{I.C.M.} = \frac{1}{n}\sqrt{\sum_{i=1}^{n}u_{c,i}^2} = 0.198~\Omega. \]
Combinamos ahora la incertidumbre estadística ($u_A$) con la I.C.M.:
\[ u_c(\bar{R}) = \sqrt{u_A^2 + (\text{I.C.M.})^2} = \sqrt{0.513^2 + 0.198^2} = 0.550~\Omega. \]
Usamos un factor de cobertura $k = 2$ (95 % de confianza) para obtener la incertidumbre expandida:
\[ U = k \, u_c(\bar{R}) = 2 \times 0.550 = 1.10~\Omega. \]
Por tanto, el resultado final del experimento es:
Este resultado concuerda con el valor nominal del fabricante (100 Ω ± 10 %), por lo que se considera compatible dentro del nivel de confianza adoptado.
Para ver la gráfica correspodiente a los datos de la tabla aquí presente, consulta la lección 6.