Lección 5. La incertidumbre típica combinada y la desviación estándar

Revisitemos un concepto que ya hemos usado un par de veces hasta ahora...

Desviación Estándar ($\sigma$):

Es una medida de la dispersión de un conjunto de datos respecto a su media. Se utiliza para caracterizar la incertidumbre de una única magnitud medida repetidamente.

Para $ n $ observaciones $ x_1, x_2, \ldots, x_n $ con media $ \bar{x} $, se calcula como:

\[ \sigma = \sqrt{\frac{1}{n-1} \sum_{i=1}^n (x_i - \bar{x})^2 } ~~~~~~~~ (5.1) \]

Esta definición aparece en muchos otros conceptos de Estadística.

Incertidumbre Típica Combinada $u_c$:

Es la desviación estándar estimada del resultado de una medición que depende de múltiples magnitudes. Combina las incertidumbres estándar de las magnitudes involucradas. Supongamos que la Potencia Eléctrica $P = VI$ con base en valores de diferencia de potencial eléctrico (también llamado $V$, voltaje) e intensidad de corriente ($I$) que medimos con nuestros instrumentos.

Consideremos antes el caso general: que nuestra medición indirecta es una función de $n$ variables $f(\bar{x})$ con $\bar{x} = (x_1, x_2, ..., x_n)$

\[ u_c = \sqrt{\sum_{i=1}^n \left( \frac{\partial f}{\partial x_i} \cdot u(x_i) \right)^2 + 2 \sum_{i=1}^n \sum_{j=i+1}^n \left( \frac{\partial f}{\partial x_i} \cdot \frac{\partial f}{\partial x_j} \cdot \text{Cov}(x_i, x_j) \right)} \]

Esto parece una fórmula muy complicada, pero no te preocupes, pues para nuestros propósitos, debido a que las fuentes de error de los parámetros son casi siempre aleatorias, no existe correlación estadística entre los errores. Si no hay correlaciones ($ \text{Cov}(x_i, x_j) = 0 $), la fórmula se simplifica a:

\[ u_c = \sqrt{\sum_{i=1}^n \left( \frac{\partial f}{\partial x_i} \cdot u(x_i) \right)^2 } \qquad (5.2) \]

donde $\frac{\partial f}{\partial x_i}$ es la derivada parcial de la función con respecto a la $i$-ésima variable y $u(x_i)$ es la incertidumbre absoluta individual asociada al instrumento con el que se tomó su medición, es decir, en este caso la mitad de la mínima escala en ditribución rectangular.

Tanto la desviación estándar como la incertidumbre típicia combinada están relacionadas por su uso en la propagación de incertidumbres:

La desviación estándar describe la incertidumbre de un conjunto de mediciones individuales. La incertidumbre típica combinada extiende este concepto para incluir múltiples fuentes de incertidumbre, ponderadas por sus efectos en el resultado.

Básicamente, usaremos la incertidumbre típica combinada para cuando queramos calcular la incertidumbre asociada a una función de varias variables (medición indirecta), como una sustitución moderna a la suma lineal de errores máximos (sección opcional de la Lección 4).

¿Por qué los coeficientes de correlación suelen ser cero en la incertidumbre combinada en un laboratorio universitario?

En la fórmula de la incertidumbre típica combinada aparece el término de la correlación entre magnitudes $Cov(x_i,x_j)$, pero en un laboratorio de la vida real, tanto universitario como profesional, la gran mayoría de las veces ese coeficiente se toma como cero. La razón es que normalmente las variables que medimos provienen de instrumentos distintos, procedimientos separados o fuentes de error independientes.

El que un valor salga un poquito más grande o más chico no afecta sistemáticamente a otro valor medido. Por ejemplo, la lectura de calibrador con un vernier no “arrastra” ni “empuja” la lectura de un reloj, ni la temperatura del laboratorio. Todo está suficientemente desconectado como para que no haya relación estadística entre ellos. Por eso, en condiciones comunes de un laboratorio, donde usamos mediciones independientes y equipos separados, lo razonable (y recomendado por la GUM cuando no hay evidencia de lo contrario) es simplemente decir que el coeficiente de correlación vale $ 0$ , lo que simplifica la fórmula y refleja la realidad de la práctica experimental básica.

Continuemos con nuestro ejemplo de la Potencia Eléctrica

Caso: Queremos medir la potencia eléctrica $ P $ (unidades: watts o vatios [$W$]) usando:

Tensión: $ V = (100.0 \pm 0.5 ) \text{V} $ (voltios)
Corriente: $ I = (2.0 \pm 0.1) \text{A} $ (amperios)

La potencia se calcula como $ P = V \cdot I $.

1. Derivadas parciales:

\[ \frac{\partial P}{\partial V} = I, \quad \frac{\partial P}{\partial I} = V \]

2. Incertidumbres absolutas individuales:

\[ u(V) = 0.5, \quad u(I) = 0.1 \]

3. Incertidumbre típica combinada:

\[ u_c(P) = \sqrt{\left( I \cdot u(V) \right)^2 + \left( V \cdot u(I) \right)^2} \]

Sustituyendo valores:

\[ u_c(P) = \sqrt{(2.0 \cdot 0.5)^2 + (100.0 \cdot 0.1)^2} = \sqrt{1.0 + 10.0} = \sqrt{11.0} \approx 3.32 \, \text{W} \]

La incertidumbre típica combinada ($ 3.32 \, \text{W} $) incluye los efectos de las incertidumbres en $ V $ e $ I $ combinadas según la propagación de incertidumbres.

Incertidumbre combinada relativa de algunas funciones

La incertidumbre típica combinada relativa es la incertidumbre combinada de una función dividida entre la función misma, es decir:

\[ \frac{u_c(f)}{f} \]

Producto

Si tenemos una función $R = R(A,B) = A \cdot B$, tenemos que:

\[ \frac{u_c (R)}{R} = \sqrt{\left( \frac{u_A}{A}\right)^2 + \left( \frac{u_B}{B} \right)^2} ~~~~ (5.3)\]

Cociente

Si tenemos una función $R = R(A,B) = \frac{A}{B}$, tenemos que:

\[ \frac{u_c (R)}{R} = \sqrt{\left( \frac{u_A}{A}\right)^2 + \left( \frac{u_B}{B} \right)^2} ~~~~(5.4); \]

que es idéntica a la incertidumbre combinda relativa del producto de $A$ y $B$.

Logaritmo natural

Si tenemos una función $R = \ln A$, tendremos que:

\[ \frac{u_c (R)}{R} = \frac{u_A}{A^2} ~~~~(5.5)\]

Potencia

Si tenemos una función $R = A^n$, tenemos que:

\[ \frac{u_c (R)}{R} = n \frac{u_A}{A} ~~~~ (5.5)\]

Ponemos a tu disposición una Calculadora de Incertidumbre Combinada. Sigue el pequeño manual de instrucciones aquí:

Tipos de incertidumbre según la GUM

Según la manera de obtención de los datos, existen tres tipos de incertidumbre combinada. Las incertidumbres se clasifican de acuerdo con cómo se obtienen los datos y de qué tipo de información proceden. De esta forma podemos distinguir tres categorías principales: Tipo A, Tipo B y la incertidumbre expandida, que a veces se denota como $U$.

Incertidumbre Tipo A

Se evalúa por métodos estadísticos, es decir, cuando se repite una medición varias veces en las mismas condiciones y los valores varían ligeramente. Proviene de la dispersión natural de los datos y se calcula con la desviación estándar de la media:

\[ u_A = \frac{s}{\sqrt{n}} \qquad (5.6), \qquad \sigma = \sqrt{\frac{\sum (x_i - \bar{x})^2}{n-1}} \qquad (5.7) \]

Cuantas más veces se mida, menor será esta incertidumbre, porque el promedio se vuelve más estable.

Ejemplo: En la Lección 2 la utilizamos en el caso de: si medimos el tiempo de caída de una pelota cinco veces y obtenemos ligeras diferencias, esa variación se analiza estadísticamente para obtener $u_A$.

Incertidumbre Tipo B. Revisitamos nuestro concepto de la Lección 2 con otro nombre.

Es la modificación de nuestro criterio original de la mitad de la mínima escala, y que ya conocemos como incertidumbre absulta, sin embargo, aquí forma parte de una sucesión de mediciones de datos experimentales. Se evalúa cuando no hay datos repetidos o cuando la información proviene de otras fuentes: manuales del fabricante, certificados de calibración, experiencia previa o resolución del instrumento. En este caso no se usa estadística experimental, sino un razonamiento basado en el conocimiento del instrumento.

Cuando se desconoce la probabilidad exacta dentro de un intervalo, la GUM recomienda suponer una distribución rectangular (uniforme):

\[ u_B = \frac{a/2}{\sqrt{3}} \quad = \frac{\text{mitad de la mínima escala}}{\sqrt{3}} \quad (5.8) \]

Esto significa que el valor verdadero tiene la misma probabilidad de encontrarse en cualquier punto del rango ±a. El Tipo B refleja la incertidumbre instrumental o sistemática.

Incertidumbre expandida ($U$)

En la práctica, el resultado final de una medición suele estar afectado por ambos tipos de incertidumbre: la aleatoria (Tipo A) y la instrumental o sistemática (Tipo B). Para expresar la incertidumbre "total" del resultado final, se combinan ambas en suma en cuadratura:

\[ U = k \cdot \sqrt{u_A^2 + u_B^2} \qquad (5.9) \]

Esta es la incertidumbre combinada.

El factor de cobertura $k$ suele tomarse como $k = 2$ porque, cuando las fuentes de incertidumbre se combinan y el resultado se comporta como una distribución normal, multiplicar la desviación estándar por 2 y usarla como rango de incertidumbre alrededor del valor medio abarca cerca del 95% de los valores posibles. En un laboratorio universitario esto es suficiente para dar un intervalo razonable de confianza sin complicar el cálculo.

La Distribución Normal

La distribución normal es una curva en forma de campana (también llamada Campana de Gauss) que describe cómo muchos datos se concentran alrededor de un valor central (media o promedio) y disminuyen hacia los extremos. En los laboratorios, los errores pequeños y aleatorios de diferentes fuentes suelen combinarse de tal manera que el resultado se ajusta bastante bien a la distribución normal.

\[ f(x) = \dfrac{1}{\sigma \sqrt{2\pi}} \, \exp\left( -\,\dfrac{(x - \mu)^2}{2\sigma^2} \right) ~~~~ (5.10) \] donde: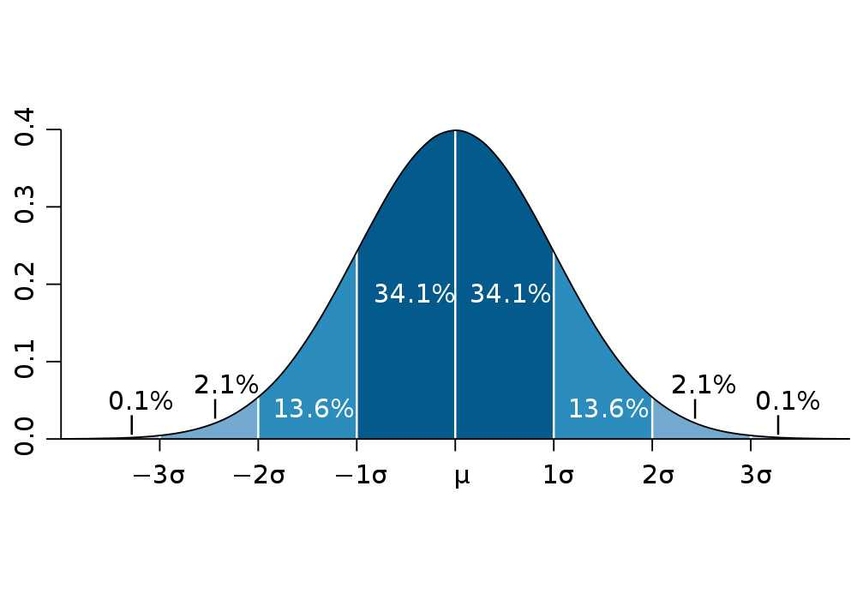

$x$: variable aleatoria continua (el “valor” que puede tomar la medición).
$f(x)$: función de densidad de probabilidad de la distribución normal en el punto $x$.
$\mu$ (mu): media o valor esperado de la distribución; indica el centro de la campana.
$\sigma$ (sigma): desviación estándar de la distribución; mide la dispersión de los valores alrededor de $\mu$.
$\pi$: número pi que ya conoces.
$\exp(\cdot)$: función exponencial, es decir, $\exp(y) = e^{y}$, donde $e \approx 2.71828$.

Distribución normal — **Figura 1: La curva de la Distribución Normal. Puedes apreciar que se cubren el 95% de los datos en un rango de $2\sigma$.**

Para propósitos de la Campana de Gauss:
$u_c$ viene representando la desviación estándar ($\sigma$) de la distribución de todos los datos analizados en el experimento después de combinar todas las contribuciones de incertidumbre y contemplando el resultado final como $\mu$, y $k$ es un factor que expande esa desviación estándar para formar un intervalo de confianza del 95%.

Si te interesa saber más sobre la fascinante Ditribución Normal, te recomendamos: Freedman, D., Pisani, R., & Purves, R. (2007). Chapter 6: The Normal Curve. En Statistics (4th ed., pp. 127–158). W. W. Norton & Company.

Volviendo a la Incertidumbre Expandida $(U)$...

Así, $U$ delimita el intervalo dentro del cual es muy probable que se encuentre el valor verdadero. Esta, la Incertidumbre expandida, es la incertidumbre "final" que queremos obtener después de nuestros experimentos.

Ejemplo:

Si para una medición $\bar{t} = 1.44 $ $u_A = 0.01~\text{s}$ y $u_B = 0.02~\text{s}$, entonces: \[ u_C = \sqrt{0.01^2 + 0.02^2} = 0.022~\text{s}, \qquad U = 2u_C = 0.044~\text{s}. \] El resultado puede expresarse como: \[ t = (1.44 \pm 0.044)~\text{s}, \quad \text{con un nivel de confianza del 95 %}. \]

Combinación de resultados con sus propias incertidumbres

Sin embargo, en la mayoría de tus experimentos, para obetner la incertidumbre asociada al promedio experimental final, no usaremos la ecuación (5.9), sino una pequña modificación introduciendo algo que llamaraemos $I.C.M.$ (Incertidumbre Combinada de la Media).

En la práctica, no siempre repetimos una misma medición directa varias veces con el mismo instrumento. A veces, cada resultado proviene de un cálculo o medición independiente (por ejemplo, cada vez se usa un conjunto de datos diferente, o se calcula una magnitud derivada con sus propias incertidumbres combinadas). En esos casos, cada valor obtenido tiene su propia incertidumbre combinada, denotada por $u_{c,i}$.

Supongamos que repetimos el experimento $n$ veces y obtenemos los resultados: \[ x_1,~x_2,~x_3,~\ldots,~x_n \] cada uno acompañado por su incertidumbre combinada $u_{c,1},~u_{c,2},~\ldots,~u_{c,n}$.

El promedio de estos resultados es: \[ \bar{x} = \frac{1}{n} \sum_{i=1}^{n} x_i \qquad (5.11) \]

Como la media es $\bar{x} = \frac{1}{n} (x_1 + x_2 + \ldots + x_n)$, cada derivada parcial es $\frac{\partial \bar{x}}{\partial x_i} = \frac{1}{n}$. Al sustituir en la ecuación (5.2), obtenemos:

\[ I.C.M. = \sqrt{\frac{1}{n^2} \sum_{i=1}^{n} u_{c,i}^2} \qquad (5.12) \] Con cada $u_{c,i}$ siendo la incertidumbre típica combinada del inicio de la lección. Esta ecuación nos da la incertidumbre combinada de la media cuando los resultados individuales ya tienen su propia incertidumbre combinada.

Nota: La “I.C.M.” (Incertidumbre Combinada de la Media) es una nombre didáctico que fue adoptado en esta guía para representar la suma en cuadratura de las incertidumbres típicas combinadas de cada iteración. En la GUM y en Bell, Stephanie (NPL Guide No. 11) esta magnitud se describe simplemente como la incertidumbre estándar del promedio cuando cada valor posee su propia incertidumbre combinada.

Tipo	Cómo se obtiene	Origen principal
A	Por estadística (repetir y calcular la dispersión)	Variación aleatoria de los datos
B	Por conocimiento del instrumento o calibración	Resolución, certificado o manual
Incertidumbre típica combinada $u_c$	Combinando las $u_B$ en cuadratura	Cada instrumento involucrado en la medición indirecta
I.C.M.	Combinando las $u_c$ de cada medición	Promedio de resultados independientes
Expandida $U$	Combinando $u_A$ y la $I.C.M.$ en cuadratura	Todas las fuentes de incertidumbre

Criterio de concordancia con el valor de referencia

Una vez que se obtiene el valor final de una magnitud experimental y su incertidumbre expandida $U$, es posible comparar el resultado con un valor de referencia.

La GUM recomienda evaluar si el resultado experimental y el valor de referencia son concordantes usando el siguiente criterio:

\[ |v_{\text{promedio}} - v_{\text{referencia}}| < U \qquad (5.13) \]

donde:

$v_{\text{promedio}}$ es el valor obtenido experimentalmente (promedio de tus mediciones).
$v_{\text{referencia}}$ es el valor teórico, certificado o tabulado con el cual se compara.
$U = k\,u_C$ es la incertidumbre expandida de tu resultado./li>

Si la diferencia entre el valor experimental y el valor de referencia es menor que la incertidumbre expandida, los resultados se consideran concordantes o compatibles dentro del margen de incertidumbre.

Por el contrario, si:

\[ |v_{\text{promedio}} - v_{\text{referencia}}| > U, \]

entonces la medición y el valor de referencia se consideran no concordantes, lo que sugiere revisar posibles fuentes de error sistemático, condiciones de medición, o la calibración del instrumento.

Nota del autor: no porque seas un estudiante de primeros semestres desprecies siempre tu resultados ante los valores de referencia. Puede que tú estés haciendo las cosas bien, y sea el valor de referencia el qeu no es exacto respecto al valor real.

Ejemplo

Un experimento para medir la aceleración de la gravedad da: \[ g_{\text{exp}} = (9.75 \pm 0.10)~\text{m/s}^2. \] El valor nominal aceptado localmente es: \[ g_{\text{ref}} = 9.81~\text{m/s}^2 \]

La diferencia es: \[ |9.75 - 9.81| = 0.06 < U = 0.10 \] Por tanto, el resultado es concordante con el valor teórico.

Esto significa que, considerando la incertidumbre del experimento, no hay evidencia suficiente para afirmar que el resultado difiere del valor de referencia. Es decir, la medición y el valor teórico son compatibles dentro del nivel de confianza elegido.

Guía rápida

Realiza todas las iteraciones de tu experimento y sus respectivas mediciones. En estas ecuaciones $n$ es tu número final de iteraciones, mientras que $i, j$ son contadores que van desde 1 hasta $n$.

Anota las incertidumbres asociadas a tus instrumentos:

Caso 1: tu instrumento no viene con manual ni incertidumbre recomendada por el fabricante. Supón una distribución rectangular y calcula la incertidumbre Tipo B: \[ u_B = \frac{(\text{mínima escala}/2)}{\sqrt{3}} \]
Caso 2: tu instrumento sí tiene una incertidumbre recomendada en su manual. Si el manual indica una incertidumbre expandida $U$ con un factor de cobertura $k$ (usualmente $k = 2$), la incertidumbre Tipo B será: \[ u_B = \frac{U}{k}. \]
Caso 3: tu instrumento cuenta con un certificado de calibración. Usa directamente la incertidumbre estándar indicada en el certificado como la Tipo B.

Si el resultado de tu experimento es una magnitud derivada (medición indirecta), es decir una función $f(x_1, x_2, ..., x_k)$ de tus mediciones, calcula la fórmula incertidumbre típica combinada de cada iteración: \[ u_c(f_i) = \sqrt{\sum^k_{j=1} \left(\frac{\partial f}{\partial x_j} \cdot u_{B,j}\right)^2}. \] Las $u_{B,j}$ son las incertidumbres Tipo B de cada variable. Para aplicar esta fórmula numéricamente, primero necesitarás tus mediciones indirectas de cada iteración
($f_i$).

Calcula cada $f_i$ con tus mediciones y su correspondiente $u_c(f_i)$ Luego obtén el promedio de los resultados: \[ \bar{f} = \frac{1}{n}\sum^n_{i=1} f_i \] Este será tu valor experimental medio.

Calcula la incertidumbre Tipo A: \[ u_A = \frac{\sigma}{\sqrt{n}}, \quad \text{donde}~~~ \sigma = \sqrt{\frac{\sum_i (f_i - \bar{f})^2}{n-1}} \]

Calcula la incertidumbre combinada de la media (I.C.M.): \[ I.C.M. = \sqrt{\frac{1}{n^2} \sum^{n}_{i=1} u^2_{c,i}}\]

Calcula la incertidumbre expandida multiplicando la combinada por el factor de cobertura $k = 2$: \[ U = k \cdot \sqrt{u_A^2 + (I.C.M.)^2} \] Esta es la incertidumbre asociada a tu resultado final.

Expresa el resultado final como: \[ f_{\text{experimental}} = (\bar{f} \pm U)\text{unidades} \quad \\ (k=2,\; \text{nivel de confianza del 95 %}) \] Al final asegúrate de redondear todo a las cifras significativas pertinentes de acuerdo a los criterios de la Lección 1.

Si tienes un valor de referencia, compara tu resultado aplicando el criterio de concordancia. Discute qué puedes concluir de tus valores obtenidos experimentalmente y sobre el valor de referencia.

Si lo deseas, puedes revisar la sustentación teórica de referencias a la GUM en el siguiente apartado:

Justificación de la Guía Rápida

Ponte a prueba

1. ¿Qué mide la desviación estándar en un conjunto de datos?

El valor promedio de los datos.
El error del instrumento.
El grado de dispersión de los valores alrededor de la media.
El número total de mediciones.

2. ¿Qué caracteriza a la incertidumbre Tipo A?

Se obtiene a partir del manual del instrumento.
Se calcula estadísticamente a partir de mediciones repetidas.
Se obtiene promediando varias incertidumbres combinadas.
Depende del factor de cobertura.

3. ¿Qué caracteriza a la incertidumbre Tipo B?

Se obtiene por información del instrumento o calibración.
Depende del número de repeticiones.
Se calcula siempre con desviación estándar.
No puede combinarse con la Tipo A.

4. ¿Cuál de los siguientes ejemplos corresponde a una incertidumbre Tipo A?

Lectura de una regla con mínima escala de 1 mm.
Variación de los tiempos medidos en cinco repeticiones de un experimento.
Error de calibración especificado en un certificado.
Resolución del multímetro.

5. ¿Qué representa la incertidumbre típica combinada $u_C$?

La suma directa de todas las incertidumbres.
La combinación cuadrática de las incertidumbres Tipo A y Tipo B.
La diferencia entre la incertidumbre mayor y la menor.
La incertidumbre del instrumento únicamente.

6. Si $u_A = 0.01$ y $u_B = 0.02$, ¿cuánto vale $u_C$?

0.01
0.02
0.022
0.03

7. ¿Qué indica el factor de cobertura $k$ en la incertidumbre expandida?

Un error aleatorio adicional.
El nivel de confianza con que se reporta el resultado.
La desviación estándar mínima.
El valor medio de la muestra.

8. Si el resultado de una medición se reporta como $x = (5.00 \pm 0.10)\text{ cm}$ con $k = 2$, ¿qué significa físicamente ese ±0.10 cm?

Es la mínima escala del instrumento.
Es el rango dentro del cual el valor verdadero tiene aproximadamente un 95 % de probabilidad de encontrarse.
Es la desviación estándar del promedio.
Es el error cometido al anotar la medición.

9. ¿Qué representa la fórmula $u(\bar{x}) = \frac{1}{n}\sqrt{\sum u_{c,i}^2}$?

El cálculo de la incertidumbre Tipo B.
La desviación estándar de una sola medición.
La incertidumbre combinada del promedio de varios resultados, cada uno con su propia $u_c$.
La propagación lineal de errores máximos.

10. Tres laboratorios diferentes midieron la misma magnitud y reportaron:
$x_1 = (10.1 \pm 0.3)$, $x_2 = (9.9 \pm 0.2)$, $x_3 = (10.2 \pm 0.4)$.
¿Cuál de las siguientes afirmaciones es correcta sobre la incertidumbre del promedio $u(\bar{x})$?

Será igual al promedio de las tres incertidumbres.
Será menor que cualquiera de las incertidumbres individuales.
Será igual a la mayor de las tres.
No puede calcularse porque las incertidumbres son distintas.

¡Excelente! Ahora veremos dos experimentos ejemplo para que observes el manejo real de datos experimentales paso a paso.

Bibliografía

Ecuación (5.2): Joint Committee for Guides in Metrology. (2008). Evaluation of measurement data: Guide to the expression of uncertainty in measurement (JCGM 100:2008). Section 5.1.2.
Ecuación (5.6): Joint Committee for Guides in Metrology. (2008). Evaluation of measurement data: Guide to the expression of uncertainty in measurement (JCGM 100:2008). Section 4.2.3.
Ecuación (5.8): Joint Committee for Guides in Metrology. (2008). Evaluation of measurement data: Guide to the expression of uncertainty in measurement (JCGM 100:2008). Section 4.3.

Figuras:

Chandler, D. L. (2012, 9 febrero). Explained: Sigma. MIT News. https://news.mit.edu/2012/explained-sigma-0209